何回カードをシャッフルすれば、トランプは十分「混ざった」と言えるのでしょうか？ 数学の確率論は私たちのこんな素朴な疑問にも答えてくれます。

私は大学1年生のときの授業でマルコフ連鎖という確率の理論に出会いました。それまでに学んできた数学を使って日常の現象が解き明かされていく様に感動し、そこから確率論の沼にはまっていきました。

本記事では、まずマルコフ連鎖を使ってカードのシャッフルを数学的に考える方法 を紹介し、最後に少しだけパーコレーションという別の理論を紹介します。あなたも確率論の世界に少しだけ足を踏み入れてみませんか？

【今井柚希・理学院修士１年】

確率的な現象を記述するマルコフ連鎖

まず、シャッフルの原理を理解する前提として、マルコフ連鎖について紹介します。マルコフ連鎖とは

• ある決まった確率に従って状態が推移していき
• 現在の情報だけから未来の情報を予測できる

もののことを言います。例えば { 晴れ, 曇り, 雨 } を状態とし，状態が遷移する確率 (推移確率) を下の図のように定めます。

例えば、一番上の行にある0.3は、今日の天気が晴れのときに明日の天気が曇りになる確率が0.3 (=60%) であることを表しています。各行 (0.6, 0.3, 0.1), (0.4, 0.4, 0.2), (0.3, 0.3, 0.4) を分布と呼びます。

では、2日後の天気がどうなるかを予測してみましょう。それは

 と計算できます。他の場合の「今日→ 2日後の確率」もこれと同じように計算し、上と同様に表してみると

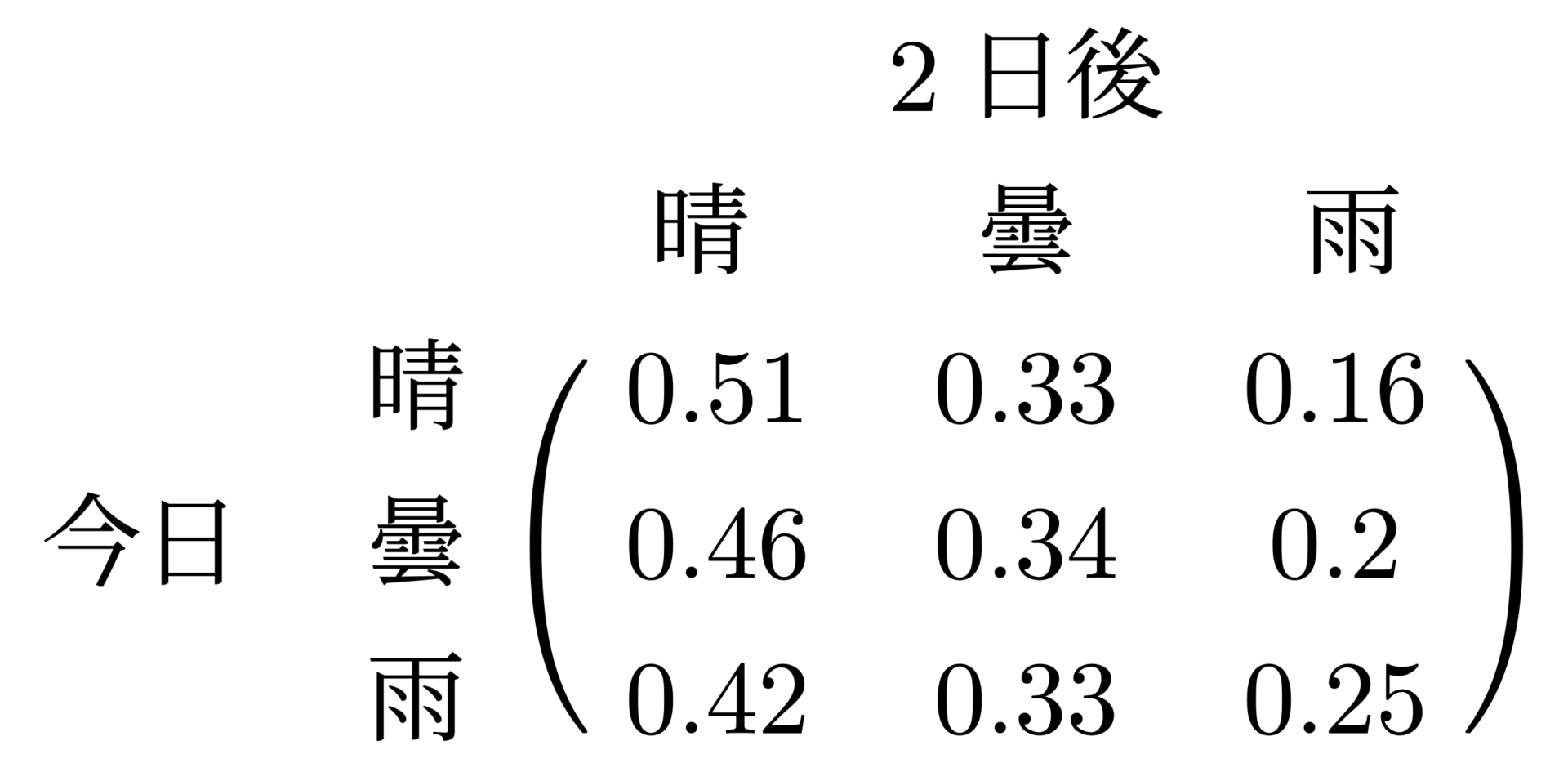
となります。

これを何度も繰り返して計算していくと、

という確率に少しずつ近づいていきます。明日晴れになる確率は、今日の天気によって異なります。しかし、「∞日後」が晴れの確率は現在の天気によらず0.48で等しいということを言っています。つまり、ものすごく先の未来になると、「現在の情報」の影響はなくなっていくのです。この分布 (0.48, 0.33, 0.19) を平衡分布と呼びます。

カードシャッフルをマルコフ連鎖で表す

では、このマルコフ連鎖を使ってカードシャッフルを数学的に表現する方法の一つを紹介します。52枚のトランプをまず半分に分けます 。もちろん、いつでもピッタリ半分に分けられるとは限りません。何枚に分かれるかは、ある決まった確率に従っているとします。次に、2つの山からカードを1枚ずつとって重ねていき、1つの山にします。詳しくいうと，山①がa枚で山②がb枚のとき，①か②からそれぞれa:bの確率でカードを1枚選んで重ねるとします。

すると、

• 52枚のカードの並び方は決まった確率に従って推移し
• 次の並び方がどうなるかは現在の並び方だけから決まる

ので、これはマルコフ連鎖と言えます。

例えばカードが3枚の場合、その状態は全部で以下の6通りあります。

このとき、同様の手順でシャッフルをすると、推移確率は

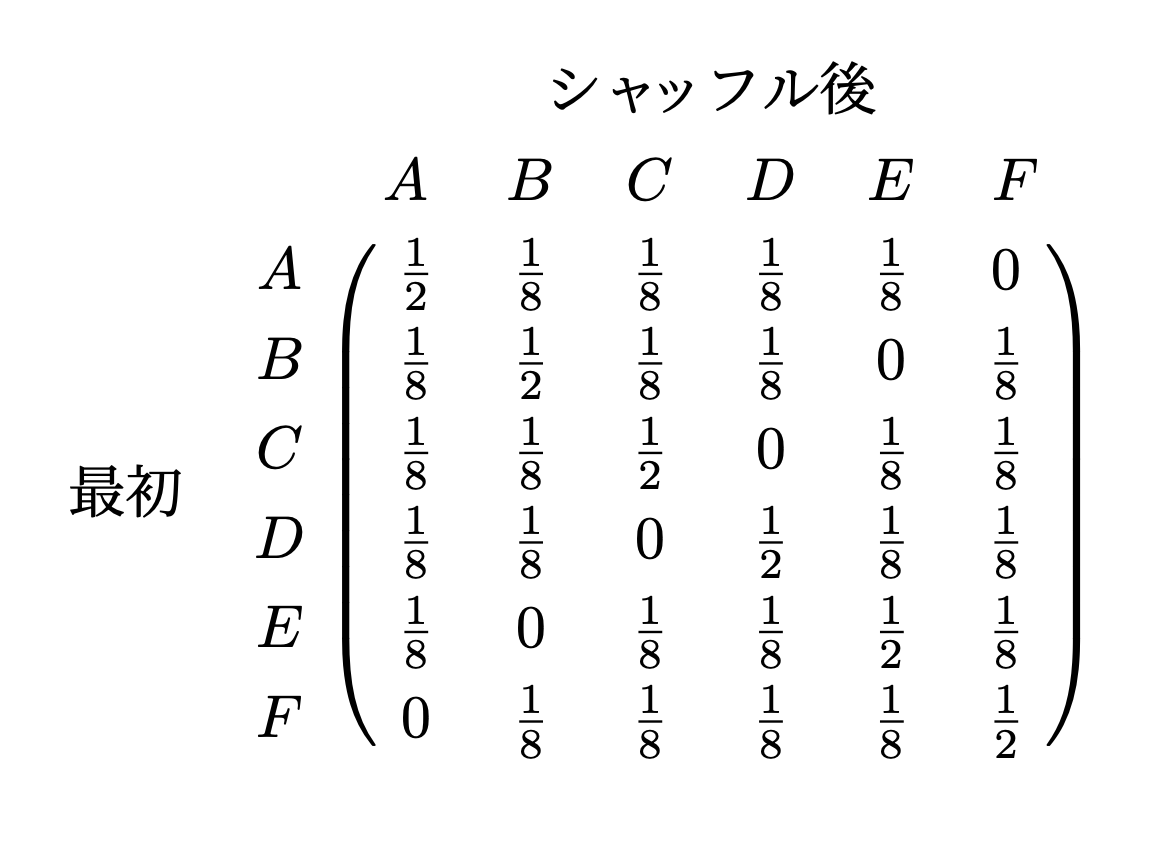
と表されます。

(1, 0, 0, 0, 0, 0) という分布、つまりシャッフル前がAの状態から始めるとすると、1回シャッフルした後は (1/2, 1/8, 1/8, 1/8, 1/8, 0) という分布に変わり、最終的には (1/6, 1/6, 1/6, 1/6, 1/6, 1/6) という平衡分布に近づいていきます。 この平衡分布を「混ざった」とします。

ここで、(1/2, 1/8, 1/8, 1/8, 1/8, 0) と (1/6, 1/6, 1/6, 1/6, 1/6, 1/6) に対してそれぞれの確率の差を計算します。1/2と1/6の差は1/3、1/8と1/6の差は1/24、0と1/6の差は1/6です。1/3と1/24を4つ、そして1/6を合計すると2/3となります。これを半分にした1/3を2つの分布の距離と呼びます。これは「1回シャッフルしたことで平衡分布にどれだけ近づいたか」を定量化したものであると考えることができます。それをグラフに表したのが下の図です。これを見ると、52枚のカードは7回程度で「混ざった」と言えそうではないでしょうか。

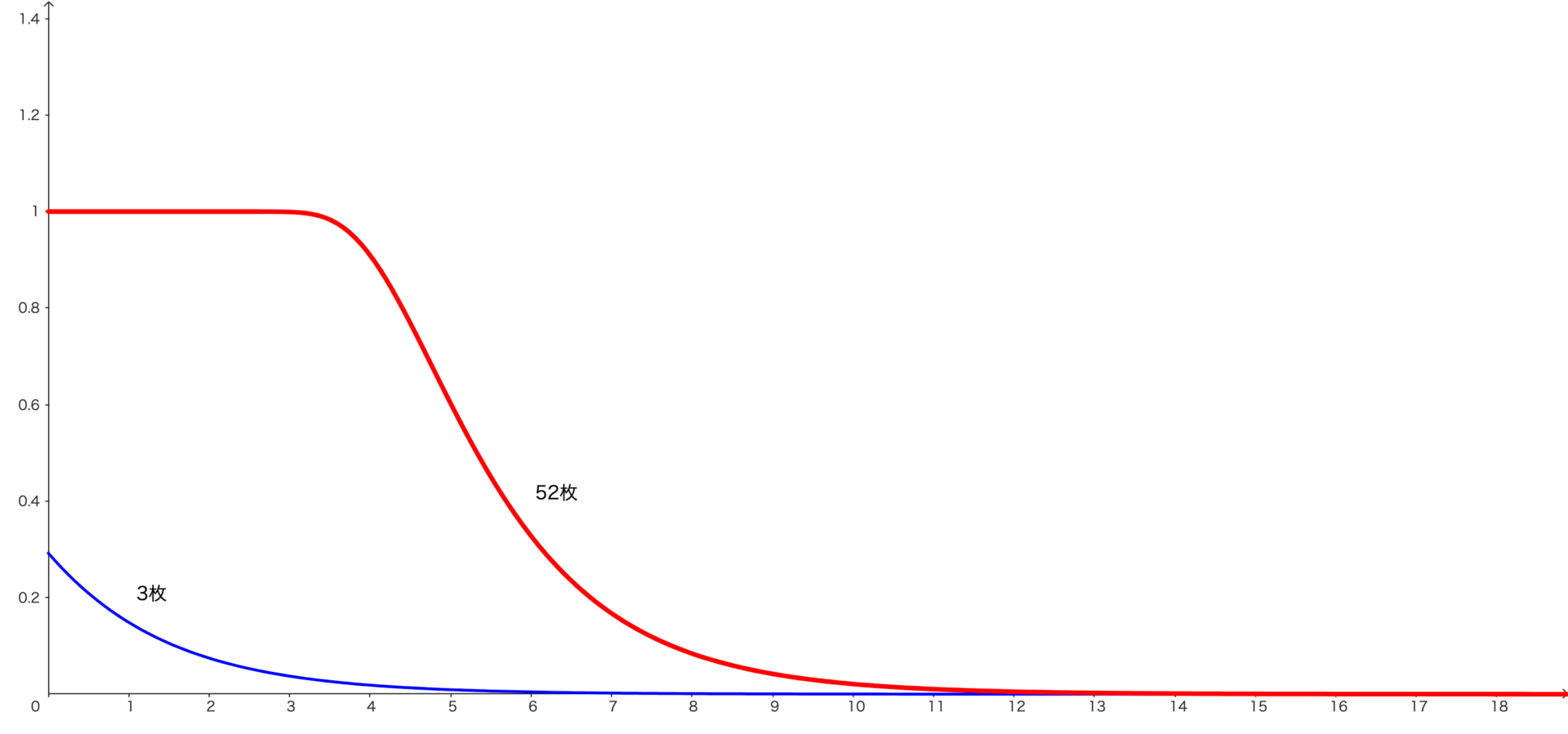
一方で、何か不思議なことに気がつきませんか？4回目まではまったく混ざり具合が変わっておらず、5回目以降で急に混ざりだしているのです。このように、各時点での分布と平衡分布の距離が急激に変化する現象をカットオフ現象 と呼びます。このカットオフ現象が私の研究の主役です。

確率の伝播を記述するパーコレーション

私の研究について語るには、もう一つの理論が不可欠です。それがパーコレーションです。直訳は「浸透」という意味で、水や信号、伝染病などの「伝播」する現象を数学的に表すモデルとして使われています。

さて、下の左の図のような格子の上の点や辺を考えます。格子上の隣り合う2点をランダムに繋いでいきます。繋げば辺の上を通れる (実線) ようになり、繋げなければ通行止め (破線) です。すると、右の図のようなものができます。ここでは、2点を繋ぐ確率を p としています。

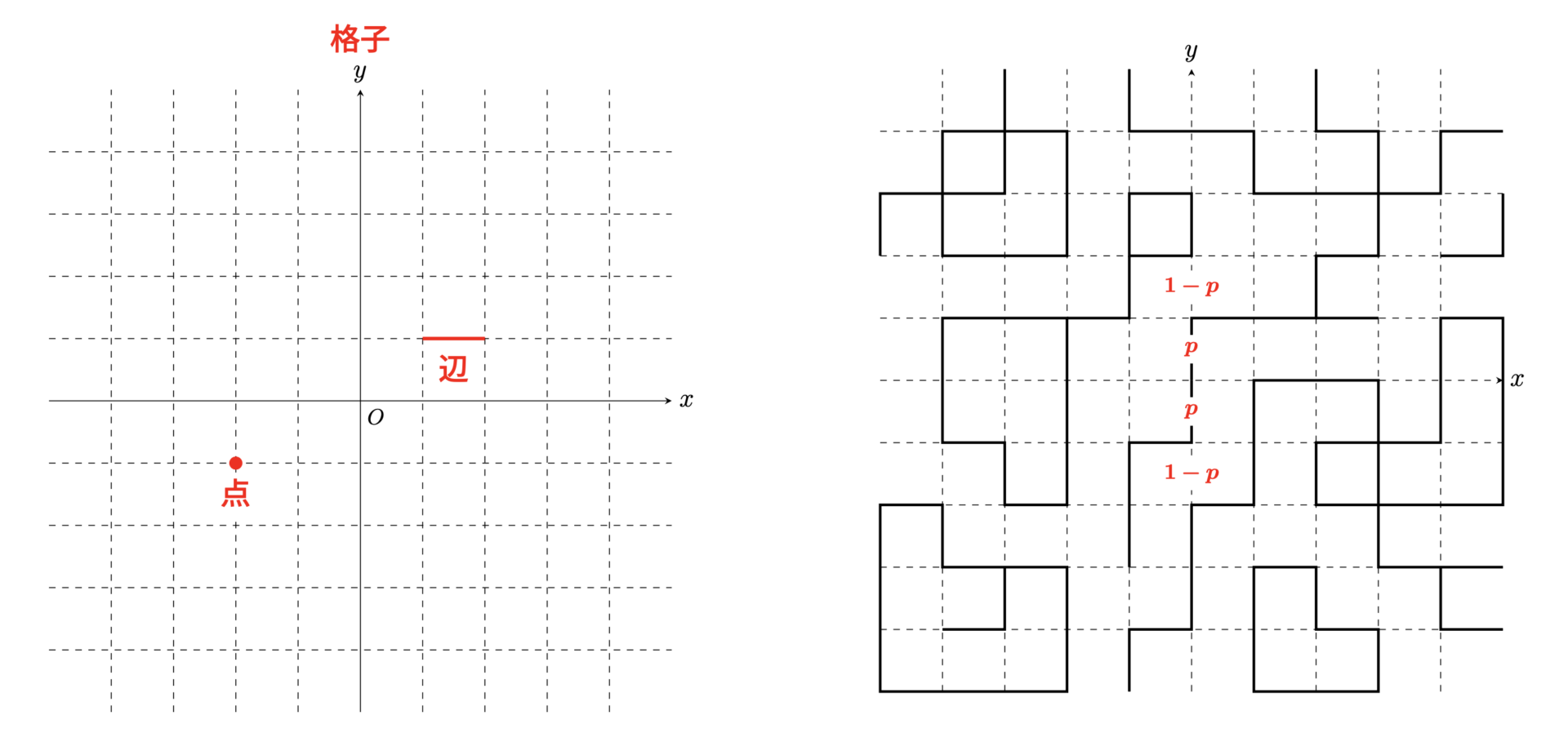
このような設定のもとで、繋がれた辺を通っていったときに「無限の彼方まで辿り着ける道が存在する確率」を考えていきます。  この点を「人」とみて「辺が通れる＝病気がうつる」とみなせば、コロナのような伝染病のモデルにも応用することもできます。この場合の「無限の彼方まで辿り着ける」という想定は「病気が蔓延する」という状況になります。

さて、数学ここで「一辺の長さが n の正方形の左辺から右辺を繋ぐ経路が存在する確率」というものを考えます。n が大きいほどこの確率は小さくなります。しかもその小さくなり方は、カットオフ現象のようにある値を境に急激に変化することが知られています。

私の目標は、マルコフ連鎖がカットオフを起こす要因で、カットオフを起こしている「犯人」を特定することです。そのために、「急激な変化」という点で似た振る舞いをみせるパーコレーションの理論を応用できないかと考えています。

紹介した2つの理論はどちらも代表的な確率の理論で、様々な現象を数学的に解析するのに幅広く利用されています。そんな2つの間を横断するような理論が構築できれば、もっと確率論の世界が広がるに違いないと信じています。