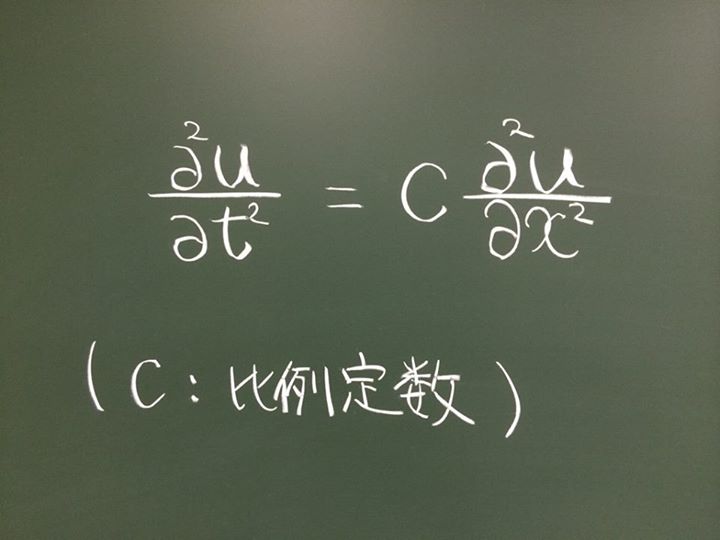私たちにとって非常に身近な自然現象である波。一見、確率とはあまり関係があるとは思えない自然現象のひとつですが、確率と大きく関わっているようです。もっと具体的に言うと、様々な波動現象は全て同じ形をした方程式を満たします。その波の方程式を波動方程式と言い、その波動方程式を満たす、様々な波動現象を表わしている解を確率的に表現できるということです。ここでは、その波動方程式の解の確率的な表現を定理としておいて、それについて説明していきます。【阿部芳彦・理学院数学専攻修士1年】
波動方程式ってなに?
まず、波動方程式について説明しましょう。波動方程式とは…
(波動方程式)
上の写真に書かれている形をした方程式のことを言います。言葉で言えば、その方程式の解である波の時間に対する二回微分は、波の空間に対する二回微分に比例するという意味です。もう少しイメージが湧くように、簡単な例でこの波動方程式を解いてみましょう。
(1次元波動方程式の解答例)
上の写真の例は、糸のようなものをx上の二点、(0,0) と (1,0) で壁に固定して動かないようにし、糸の中央を指で上に1/2だけ最初にひっぱり上げた状態から、糸を離して振動させた、という現象をイメージしてもらえるといいと思います。ここで挙げたのはあくまで例ですが、このようにして波動方程式の解を求めることが出来ます。
解の確率的表現ってどういうこと?
波動方程式について、少し知って頂けたかと思いますが、それでは、その波動方程式の解を確率的に表現するとはどういうことなのでしょうか?大雑把に言ってしまうと、例えば、花粉の粒子を水に落とすと、目に見えない無数の水分子と衝突してジグザグに運動します(ブラウン運動)。このようなランダムな運動に沿った粒子の輸送の期待値として、その方程式の解を記述するということです。実際にそのようにして、波動方程式の解を表現したのが、次に記す定理となります。
定理の紹介
波動方程式の解の確率的表現の定理を紹介します。
(定理)
記号ばかりで良く分からないかもしれませんが、要するに、上の定理のように解を確率的に表現すると、波動方程式を満たす解となっているということです。ここでは、この定理についてあまり深く説明するつもりはありませんが、証明やもっと深く理解したい方は〝参考文献[1]″を検索して、そちらを参照して下さい。さっぱりだ…という方、諦めることなかれ! もう少しわかり易くなるように、この定理を用いて具体的な例を計算してみましょう。例えば、次元 d=1、領域 D=(-1,1)、関数 f(t,x)=exp{x}cos tとして計算すると…
(計算例)
上の写真のように計算でき、解を求めることが出来ます。もちろん、この解は波動方程式の解になっていることは、計算すれば確かめることが出来ます。少しイメージをつかめて頂けたでしょうか?
定理の問題点と今後の課題について
問題点として挙げられるのは、先ほど述べた定理によって、多くの波動方程式の解を確率的に表現できたわけですが、実はこの定理では、波動方程式の全ての解を確率的に表現できたとは言えないという点です。また、上記の波動方程式の解法の例でも挙げたように、初期値が与えられている波動方程式を解く確率的表現が本当は望ましいのですが、それもこの定理では満たしていません。これらの問題が起こる要因は様々ありますが、それらを上手く解決して、波動方程式を満たす全ての解の確率的表現を与えることが今後の課題であると言えるでしょう。
今後の私の研究
今年度、修士1年になった私は今、Parabolic Anderson Model というモデルに興味を持ち、いくつかのテキストを参照しながら日々学習しています。このモデルは、不純物を含む結晶状の電子の振る舞いであったり、ランダムに噴き出す触媒が存在する環境下での反応物の増大など、非常に興味深い現象を表わすモデルです。この Parabolic Anderson Model についてのセミナーを、週に1度、指導教官の先生や先輩、同期の学生に様々な指導やアドバイスを頂きながら行っています。わからないことが多すぎて非常に辛く、空いている時間はほぼこのセミナーの準備で消えてしまいますが、自分を磨くという部分でも、とてもいい機会だと思うので、自分なりに辛抱強く取り組んでいます。このモデルを少しでも深く理解できるように、これからの学生生活を同じ研究室の皆さんと共に、日々努力していきたいと思っています。
(最近行われた私のセミナー中の風景)
参考文献
[1] Sourav Chatterjee (2013) Stochastic solution of the wave equation.[2] Base,R.F. (1995).Probabilistic techniques in analysis. Springer Verlag.
※ ※ ※ ※ ※
この記事は、阿部芳彦さん(理学院修士1年)が、大学院共通授業科目「大学院生のためのセルフプロモーション1」の履修を通して制作した成果です。